本篇对OpenGL学习过程中遇到的关键的矩阵运算做一个总结，方便以后查阅。

文章目录

向量
- 向量计算
  - 向量和标量的运算
  - 向量加减
  - 向量长度
  - 向量乘法
    - 点乘
    - 叉乘
- 向量标准化
矩阵
- 矩阵的加减
  - 矩阵与标量相加减
  - 矩阵与矩阵相加减
- 矩阵的数乘
- 矩阵相乘
- 矩阵与向量相乘
- 单位矩阵
- 矩阵的逆
  - 余子式和代数余子式
  - 伴随矩阵
  - 逆矩阵
应用

向量

向量高中就接触了，这个问题应该不大，向量就是一个有方向的量，具有平移不变性，因此我们可以默认所有的向量都是以0点为起点，这样就可以只用一个点就表示出一个向量了。

向量计算

向量和标量的运算

向量可以和标量进行加减乘除取反等运算，依次用向量的各个标量去和标量进行运算就可以了，这个不多说，下面给出加法的例子，减乘除取反也是一样
(123)+3=(1+32+33+3)=(456) \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) + 3 = \left( \begin{array}{ccc} 1+3 \\ 2+3 \\ 3+3 \end{array} \right)= \left( \begin{array}{ccc} 4 \\ 5 \\ 6 \end{array} \right) ⎝⎛123⎠⎞+3=⎝⎛1+32+33+3⎠⎞=⎝⎛456⎠⎞

向量加减

和向量与标量的加减法计算差不多，各个分量对应运算即可。
(123)+(456)=(1+42+53+6)=(579) \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) + \left( \begin{array}{ccc} 4 \\ 5 \\ 6 \end{array} \right) = \left( \begin{array}{ccc} 1+4 \\ 2+5 \\ 3+6 \end{array} \right)= \left( \begin{array}{ccc} 5 \\ 7 \\ 9 \end{array} \right) ⎝⎛123⎠⎞+⎝⎛456⎠⎞=⎝⎛1+42+53+6⎠⎞=⎝⎛579⎠⎞
向量减法有个特性在OpenGL中会经常用到，我们看下图：

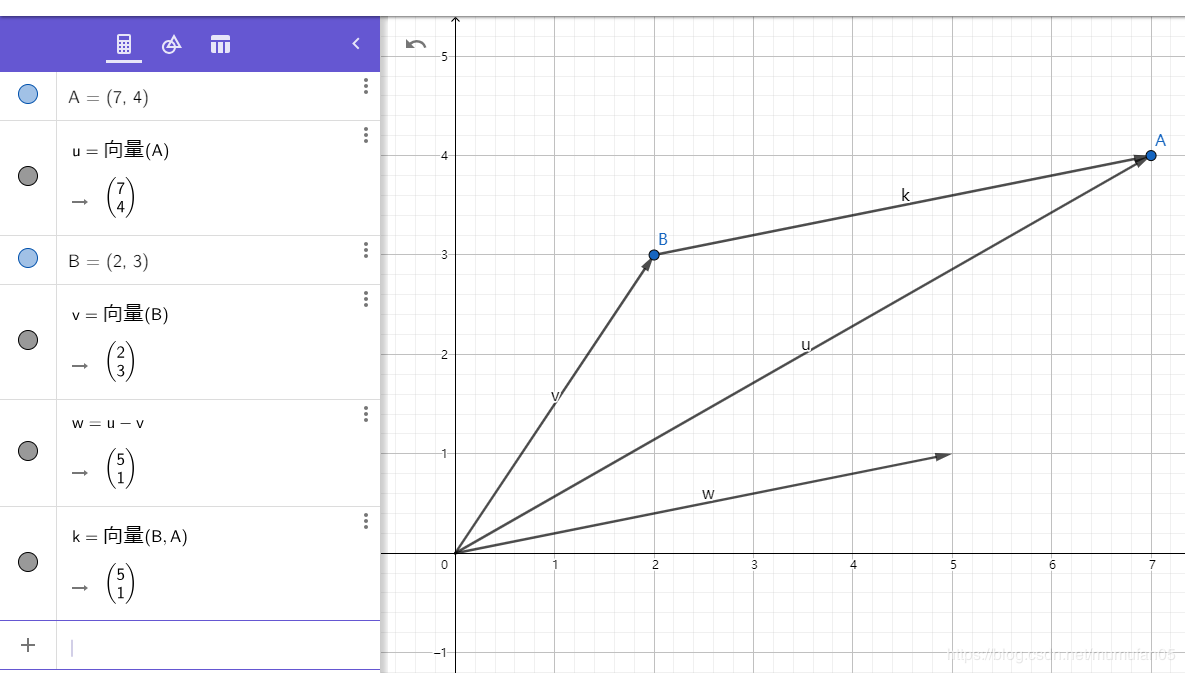
上图是一个向量减法的计算，w⃗=u⃗−v⃗\vec{w}= \vec{u}-\vec{v}w=u−v，我们再将w⃗\vec{w}w平移至k⃗\vec{k}k，可以看到向量k⃗\vec{k}k的方向就是B点指向A点的方向，这个特性在OpenGL控制摄像机的朝向时候会用到。

向量长度

向量长度又叫向量的模，用|v|表示，这个也没啥难度，用勾股定理就能算，看下下图就懂了
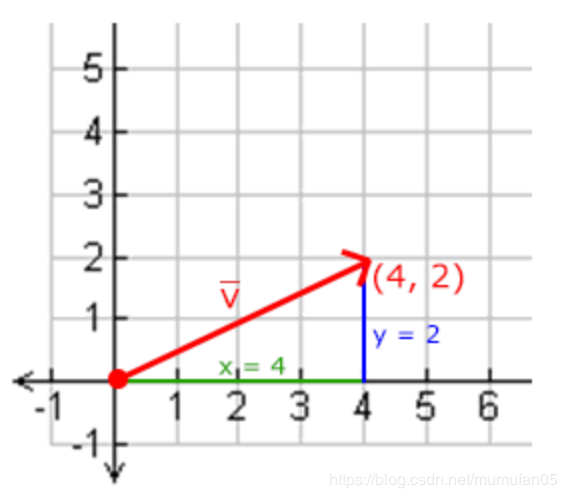
勾股定理计算向量的长度

向量乘法

向量的普通乘法没有意义，但是可以有点乘和叉乘：点乘(Dot Product)，记作v⃗⋅k⃗\vec{v} \cdot \vec{k}v⋅k；叉乘(Cross Product)，记作v⃗×k⃗\vec{v} \times\vec{k}v×k

点乘

点乘的公式：

v⃗⋅k⃗=∣v⃗∣⋅∣k⃗∣⋅cosθ\vec{v}⋅\vec{k}=

\vec{v}

⋅

\vec{k}

⋅cosθv⋅k=∣v∣⋅∣k∣⋅cosθ

如果把这个公式变形可以用来计算向量的夹角
cosθ=v⃗⋅k⃗∣v⃗∣⋅∣k⃗∣ cosθ = \dfrac{\vec{v}⋅\vec{k}}{|\vec{v}|⋅|\vec{k}|} cosθ=∣v∣⋅∣k∣v⋅k
那怎么计算v⋅k呢？就是各个分量依次相乘，再将结果相加，如下面的向量
(123)⋅(456)=(1×4)+(2×5)+(3×6)=32 \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) \cdot \left( \begin{array}{ccc} 4 \\ 5 \\ 6 \end{array} \right) = (1\times4)+(2\times5)+(3\times6)=32 ⎝⎛123⎠⎞⋅⎝⎛456⎠⎞=(1×4)+(2×5)+(3×6)=32
则这两个向量的夹角的余弦值就是
cosθ=v⃗⋅k⃗∣v⃗∣⋅∣k⃗∣=32∣v⃗∣⋅∣k⃗∣ cosθ = \dfrac{\vec{v}⋅\vec{k}}{|\vec{v}|⋅|\vec{k}|} =\dfrac{32}{|\vec{v}|⋅|\vec{k}|} cosθ=∣v∣⋅∣k∣v⋅k=∣v∣⋅∣k∣32
好吧，v⃗\vec{v}v和k⃗\vec{k}k的模我就不算了，领会精神
公式推导如下图
在这里插入图片描述

叉乘

叉乘只在3D空间中有定义，它需要两个不平行向量作为输入，生成一个正交于两个输入向量的第三个向量。
在摄像机章节中，我们用到了一个glm::lookAt函数来设置摄像机，该函数有三个参数，分别是摄像机位置、摄像机观察的位置和上向量。而摄像机实际上还需要一个指向方向向量和一个右向量，其中，方向向量是用目标的位置向量和摄像机位置向量做差得到的，右向量就是用上向量和方向向量进行叉乘得到的。
下图是推导过程
在这里插入图片描述
整理成矩阵格式就是
(AxAyAz)×(BxByBz)=(Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx) \left( \begin{array}{ccc} A_x \\ A_y \\ A_z \end{array} \right) \times \left( \begin{array}{ccc} B_x \\ B_y \\ B_z \end{array} \right)= \left( \begin{array}{ccc} A_y \cdot B_z-A_z \cdot B_y\\ A_z \cdot B_x-A_x \cdot B_z\\ A_x \cdot B_y-A_y \cdot B_x\\ \end{array} \right) ⎝⎛AxAyAz⎠⎞×⎝⎛BxByBz⎠⎞=⎝⎛Ay⋅Bz−Az⋅ByAz⋅Bx−Ax⋅BzAx⋅By−Ay⋅Bx⎠⎞

向量标准化

模长为1的向量通常成为标准向量，向量标准化就是求与该向量方向相同，模长为1的向量，即求向量方向上的标准向量，计算方法如下图，下图截取自同济版高数教材第七版下册
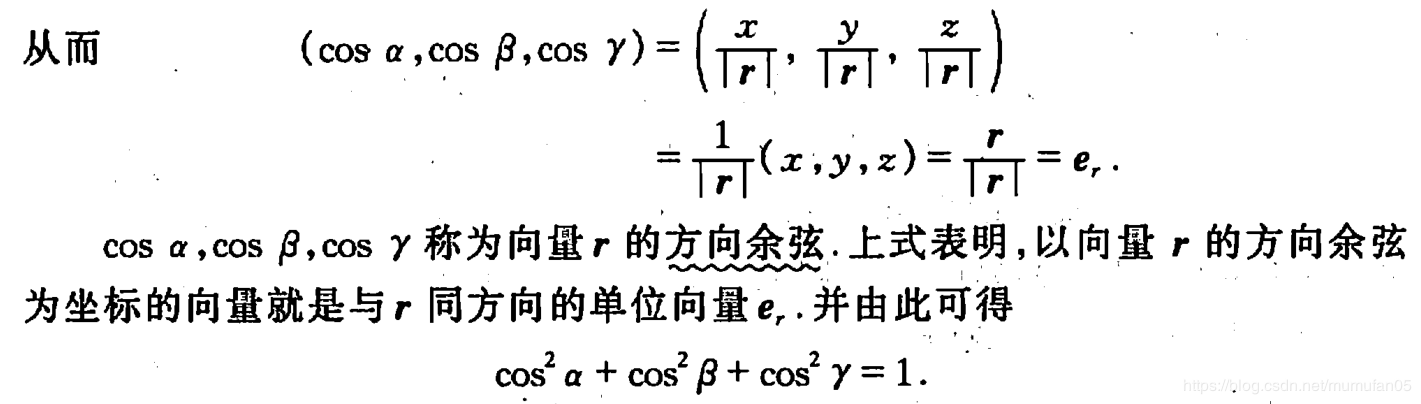
在这里插入图片描述

矩阵

矩阵的数学定义我这里就不说了（其实是不会-_-!），我觉得只要学过的人就算时间再久再怎么忘了，只要见到应该还认识，矩阵就长这样
(123456) \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 &6\end{array} \right) (142536)
这是一个2行3列的矩阵，记作2 ×\times× 3

矩阵的加减

矩阵与标量相加减

和向量一样，所有元素依次相加减即可
(1234)+3=(1+32+33+34+3)=(4567) \left( \begin{array}{ccc} 1 & 2 \\ 3 &4 \end{array} \right) + 3 = \left( \begin{array}{ccc} 1+3 & 2+3 \\ 3+3 & 4 + 3 \end{array} \right)= \left( \begin{array}{ccc} 4 & 5 \\ 6 & 7 \end{array} \right) (1324)+3=(1+33+32+34+3)=(4657)

矩阵与矩阵相加减

和向量一样，各个对应元素依次相加减即可
(1234)+(5678)=(1+52+63+74+8)=(681012) \left( \begin{array}{ccc} 1 & 2 \\ 3 &4 \end{array} \right) + \left( \begin{array}{ccc} 5 & 6 \\ 7 &8 \end{array} \right) = \left( \begin{array}{ccc} 1+5 & 2+6 \\ 3+7 & 4 + 8 \end{array} \right)= \left( \begin{array}{ccc} 6 & 8 \\ 10 & 12 \end{array} \right) (1324)+(5768)=(1+53+72+64+8)=(610812)

矩阵的数乘

同样的，所有元素依次相乘，标量就是用它的值缩放(Scale)矩阵的所有元素。
(1234)×3=(1×32×33×34×3)=(36912) \left( \begin{array}{ccc} 1 & 2 \\ 3 &4 \end{array} \right) \times 3 = \left( \begin{array}{ccc} 1\times3 & 2\times3 \\ 3\times3 & 4 \times 3 \end{array} \right)= \left( \begin{array}{ccc} 3 & 6 \\ 9 & 12 \end{array} \right) (1324)×3=(1×33×32×34×3)=(39612)

矩阵相乘

关于矩阵相乘，两个前提条件一定要注意

只有当左侧矩阵的列数与右侧矩阵的行数相等，两个矩阵才能相乘。即Am×n⋅Bn×l=Cm×lA_{m\times n} \cdot B_{n\times l}=C_{m\times l}Am×n⋅Bn×l=Cm×l
矩阵相乘不遵守交换律(Commutative)，也就是说A⋅B≠B⋅AA \cdot B \neq B \cdot AA⋅B̸=B⋅A。
设0矩阵为OOO，A⋅B=OA \cdot B=OA⋅B=O不能推出A=OA=OA=O或B=OB=OB=O。同样，若A≠OA \neq OA̸=O，而A⋅(X−Y)=OA\cdot(X-Y)=OA⋅(X−Y)=O也不能得出X=YX=YX=Y的结论，例如
(24−3−6)⋅(−241−2)=(0000) \left( \begin{array}{ccc} 2 & 4 \\ -3 &-6 \end{array} \right) \cdot \left( \begin{array}{ccc} -2 & 4 \\ 1 &-2 \end{array} \right) = \left( \begin{array}{ccc} 0 & 0 \\ 0 &0 \end{array} \right) (2−34−6)⋅(−214−2)=(0000)

矩阵相乘的公式也好蛋疼，我们用一个例子来说明矩阵相乘是怎么算的
(123456)⋅(789101112)=(1×7+2×9+3×111×8+2×10+3×124×7+5×9+6×114×8+5×10+6×12)=(5864139154) \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 &5 &6 \end{array} \right) \cdot \left( \begin{array}{ccc} 7 & 8 \\ 9 &10 \\ 11 &12 \end{array} \right) = \left( \begin{array}{ccc} 1\times7+2\times9+3\times11&1\times8+2\times10+3\times12 \\ 4\times7+5\times9+6\times11&4\times8+5\times10+6\times12 \end{array} \right)= \left( \begin{array}{ccc} 58 & 64 \\ 139 & 154 \end{array} \right) (142536)⋅⎝⎛791181012⎠⎞=(1×7+2×9+3×114×7+5×9+6×111×8+2×10+3×124×8+5×10+6×12)=(5813964154)
从这个例子可以看出为什么矩阵相乘要求左侧列数等于右侧行数了，如果不相等则没法计算，也能看出为什么结果矩阵的行数等于左侧的行数，结果矩阵的列数等于右侧的列数了
这个计算方法很是蛋疼，幸运的是我们可以把这个计算过程交给电脑去做，下面是推导过程
设有两个线性变换
在这里插入图片描述

矩阵与向量相乘

向量就是一个具有N行1列的矩阵，矩阵与向量相乘遵守矩阵与矩阵相乘的法则，这里不再多说，只要注意矩阵的行列数即可

单位矩阵

单位矩阵就是对角线上的元素都是1，其他元素都是0的矩阵，这货长这样
(1000010000100001) \left( \begin{array}{ccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) ⎝⎜⎜⎛1000010000100001⎠⎟⎟⎞
这是一个4×44\times44×4的矩阵，为毛这或叫单位矩阵呢？我们来看下下面的矩阵相乘
(1000010000100001)×(1234)=(1×1+0×2+0×3+0×40×1+1×2+0×3+0×40×1+0×2+1×3+0×40×1+0×2+0×3+1×4)=(1×11×21×31×4)=(1234) \left( \begin{array}{ccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \times \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \\ 4 \end{array} \right) = \left( \begin{array}{ccc} 1\times1+0\times2+0\times3+0\times4 \\ 0\times1+1\times2+0\times3+0\times4 \\ 0\times1+0\times2+1\times3+0\times4 \\ 0\times1+0\times2+0\times3+1\times4 \end{array} \right)= \left( \begin{array}{ccc} 1\times1 \\ 1\times2 \\ 1\times3 \\ 1\times4 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \\ 4 \end{array} \right) ⎝⎜⎜⎛1000010000100001⎠⎟⎟⎞×⎝⎜⎜⎛1234⎠⎟⎟⎞=⎝⎜⎜⎛1×1+0×2+0×3+0×40×1+1×2+0×3+0×40×1+0×2+1×3+0×40×1+0×2+0×3+1×4⎠⎟⎟⎞=⎝⎜⎜⎛1×11×21×31×4⎠⎟⎟⎞=⎝⎜⎜⎛1234⎠⎟⎟⎞
单位矩阵和任何矩阵相乘结果都等于原矩阵，类似于乘法计算中1和任何数相乘结果都是原数一样。

矩阵的逆

余子式和代数余子式

在n阶行列式中，把(i,j)(i,j)(i,j)元aija_{ij}aij所在的地iii行和第jjj列划去后，留下来的n−1n-1n−1阶行列式叫做(i,j)(i,j)(i,j)元aija_{ij}aij的 余子式 ，记作MijM_{ij}Mij；记
Aij=(−1)i+jMijA_{ij}=(-1)^{i+j}M_{ij}Aij=(−1)i+jMij
AijA_{ij}Aij叫做(i,j)(i,j)(i,j)元aija_{ij}aij的 代数余子式 ，例如四阶行列式
D=∣a11a12a13a14a21a22a23a24a31a32a33a34a41a42a43a44∣ D=\left| \begin{array}{ccc} a_{11} &a_{12} & a_{13} &a_{14} \\ a_{21} &a_{22} & a_{23} &a_{24} \\ a_{31} &a_{32} & a_{33} &a_{34} \\ a_{41} &a_{42} & a_{43} &a_{44} \\\end{array} \right| D=∣∣∣∣∣∣∣∣a11a21a31a41a12a22a32a42a13a23a33a43a14a24a34a44∣∣∣∣∣∣∣∣
中(3,2)(3,2)(3,2)元a32a_{32}a32的余子式和代数余子式分别为
M32=∣a11a13a14a21a23a24a41a43a44∣ M_{32}=\left| \begin{array}{ccc} a_{11} & a_{13} &a_{14} \\ a_{21} & a_{23} &a_{24} \\ a_{41} & a_{43} &a_{44} \end{array} \right| M32=∣∣∣∣∣∣a11a21a41a13a23a43a14a24a44∣∣∣∣∣∣
A32=(−1)3+2M32=−M32 A_{32}=(-1)^{3+2}M_{32}=-M_{32} A32=(−1)3+2M32=−M32

伴随矩阵

由n阶方阵A的元素所构成的行列式（各元素的位置不变），称为方阵A的行列式，记作det A 或|A|。
行列式|A|的各个元素的代数余子式AijA_{ij}Aij所构成的如下的矩阵
A∗=(A11A12⋯An1A12A22⋯An2⋮⋮ ⋮A1nA2n⋯Ann) A^*=\left( \begin{array}{ccc} A_{11} & A_{12} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \\ \end{array} \right) A∗=⎝⎜⎜⎜⎛A11A12⋮A1nA12A22⋮A2n⋯⋯ ⋯An1An2⋮Ann⎠⎟⎟⎟⎞
称为矩阵A的伴随矩阵，简称伴随阵

逆矩阵

在这里插入图片描述

求逆矩阵的过程：首先将矩阵写成行列式，然后求行列式的所有代数余子式，再将所有的代数余子式组合成新的矩阵（注意行列变化），即求伴随矩阵，最后用行列式的倒数乘以伴随矩阵。

应用

具体应用看下篇OpenGL学习笔记：数学基础和常用矩阵总结（二）